等ウェイト投資戦略についての一考察

1．はじめに

本年3月24日より、読売新聞社は新たな株価指数「読売株価指数（以下、読売333）」の公表を開始した。この指数は、読売新聞が独自に選定した日本国内の証券取引所に上場する333銘柄の株式を、等金額で構成・運用するという特徴を有している。同社はこの新指数について、「日経平均株価（225種）や東証株価指数（TOPIX）とは異なる視点から、日本企業の成長を捉える新たな『ものさし』となることを目指す」⑴との方針を示しており、従来の代表的な株価指数とは一線を画すアプローチを採用している。

このような等ウェイト型の投資戦略は、学術的にも長年にわたり議論の対象となってきた。特に、各銘柄に対して均等な資金配分を行う「等ウェイト（equal-weight）戦略」あるいは「1/N戦略」と呼ばれる手法は、時価総額加重型のポートフォリオと比較して、リスク分散効果やリバランスによる収益向上の可能性など、複数の観点からその有効性が検証されている。

本稿では、こうした等ウェイト投資戦略に焦点を当て、その理論的背景、実証的成果、並びに市場構造との関係性について、既存の文献レビューを通じて包括的に検討する。特に、読売333のような新指数の登場が、投資家のポートフォリオ構築や市場評価の枠組みにどのような影響を与え得るのかについて、学術的な視座から考察を試みたい。

2．読売333とは

一般的な等ウェイト投資戦略の考察に先立ち、本稿ではまず読売333の定義及びその構造的特徴について検討する。既に述べたように、読売333は、読売新聞社が選定した日本国内の証券取引所に上場する333銘柄を、等金額で構成・運用した場合の価値（円建て）を示す株価指数である。基準値は1985年11月、すなわちバブル景気前の水準を10,000円として設定されており、長期的な企業成長の可視化を意図した設計となっている。

この指数の最大の特徴は、各構成銘柄の組入比率が均等である点にある。すなわち、時価総額や1株当たりの株価に依存せず、全ての銘柄が同一の重みで評価されるため、特定の大型株や値嵩株の値動きに左右されにくい構造を持つ。読売新聞社はこの点について、「時価総額や1株当たりの株価に関係なく、どの銘柄も同じ重みで捉えているため、時価総額が大きい『大型株』や、1株当たりの株価が高い『値がさ株』といった特定の銘柄の値動きに左右されにくい特徴があ」ると説明している。実際、日経平均株価では上位5銘柄の構成比率が約31％、TOPIXでも約15％を占めるのに対し⑵、読売333では等ウェイト構成により、上位5社の合計比率はわずか約1.5％にとどまる。これは、指数全体が特定銘柄に依存せず、より広範な市場の動向を反映する設計であることを示している。

この構成方式の帰結として、読売333は他の主要株価指数と比較して、小型株の比率が相対的に高くなる傾向がある。これは指数の定義からほぼ自明であり、実際にインターネット上のノート『読売333指数の特性分析』⑶では、Russell/Nomura日本株インデックスを用いたスタイル分解（Value/Growthおよび大型／小型の軸）を通じて、読売333のスタイル特性が定量的に分析されている。同ノートでは、読売333が「TOPIXのサブ指数的な特性を持ち、日経225と補完関係にある株価指数」と位置づけられており、直感的な理解にとどまらず、データに基づいた構造的な特徴の解明が試みられている点は注目に値する。

さらに、小型株中心のポートフォリオは、理論的にも高い期待リターンを示す傾向があることが、ファーマ・フレンチの3ファクターモデルやその後の拡張モデルにおいて繰り返し確認されている。こうした理論的背景を踏まえると、読売333の構成がもたらすリターン特性やリスクプロファイルは、従来の加重型指数とは異なる投資機会を提供する可能性がある。

図表1では、読売333のデータ取得可能初日である2025年3月27日を基準値1として、同年9月10日までの主要株価指数の推移を比較している。これにより、読売333の短期的な市場反応や他指数との乖離を視覚的に把握することが可能となる。

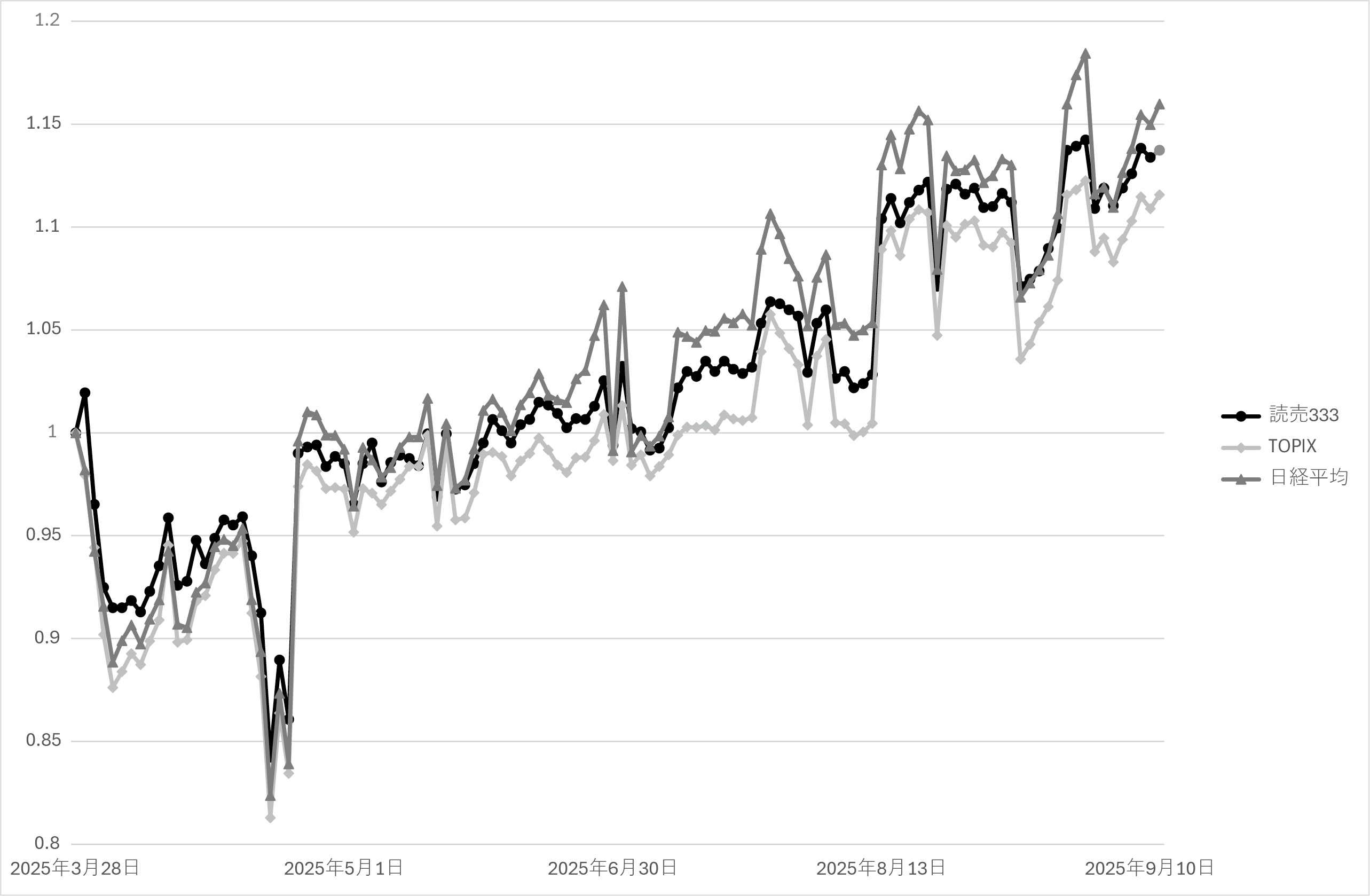
図表1の推移から明らかに読み取れるように、読売333の公表後約半年間のパフォーマンスは、日経平均株価よりも低く、TOPIXよりは高い水準で推移している。この観察結果は、読売333のスタイル特性に関する先述の分析――すなわち「TOPIXのサブ指数的な特性を持ち、日経225と補完関係にある株価指数」とする位置づけ――と整合的である。読売333がTOPIXよりも高いリターンを示した背景には、小型株比率の高さやリバランス効果が寄与している可能性がある。一方で、日経平均株価の急伸に対しては、大型値嵩株の影響が大きく、読売333はその恩恵を受けにくい構造であるため、相対的に控えめな上昇にとどまったと解釈できる。

上のグラフと同期間の日次価格データを用いて期待収益率・ボラティリティ・シャープ比率を計算したのが以下の図表2である。

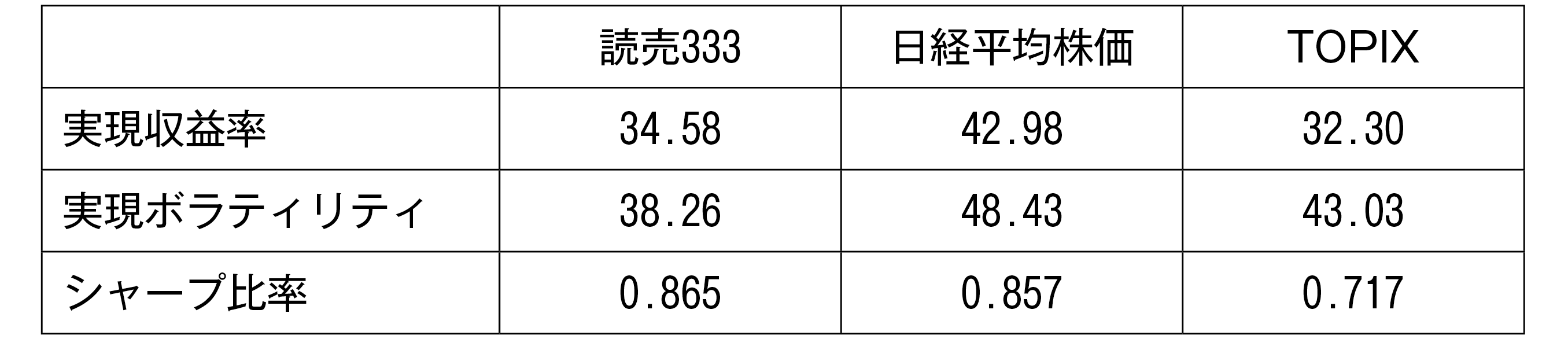
資本資産価格モデル（Capital Asset Pricing Model，以下CAPM）においては、投資家が市場全体の株式を時価総額加重平均で保有することが最適とされており、その結果として市場ポートフォリオのシャープ比率が理論的に最も高くなるとされている。これは、CAPMが前提とする完全市場、投資家の合理性、同一の期待収益率に基づく均衡条件などに依拠した結論である。

しかしながら、図表2の結果が示すように、分析期間が半年程度と短期である点を踏まえても、単純な等ウェイト投資戦略が時価総額加重型であるTOPIXのパフォーマンスを上回っている事実は注目に値する。これは、現実の市場においてCAPMの理論的前提が必ずしも成立していないことを示唆しており、理論と実証の乖離を考察する契機となる。

特に、CAPMが仮定する以下の条件――全ての投資家が同一の情報にアクセスでき、同一の期待収益率を持ち、リスク回避的であり、無リスク資産への自由なアクセスが可能である――は、現実の市場環境ではしばしば満たされない。加えて、取引コスト、税制、流動性制約、情報の非対称性などの要因が、理論モデルの成立を妨げる要因として作用していると考えられる。このようなCAPMの限界については、既に1970年代から批判的な議論が展開されており、特にRoll（1977）による指摘はその代表的なものとして知られている。Rollは、CAPMの実証的検証が困難である根本的な理由として、「真の市場ポートフォリオ」が観測不可能である点を挙げ、実際に用いられる市場指数（例えばS&P500やTOPIXなど）が理論上の市場ポートフォリオを正確に代替していない可能性を強調した。この批判は、CAPMの検証可能性そのものに疑義を呈するものであり、以後の資産価格理論において多因子モデルや行動ファイナンスの発展を促す契機となった。

このような問題意識を踏まえ、以下では等ウェイト投資戦略に焦点を当て、特に時価総額加重平均を用いた従来型の投資戦略との比較を通じて、その構造的特徴や実証的な有効性について、既存の学術研究から得られた知見を参照しながら議論を展開する。等ウェイト戦略が持つリバランス効果、分散性の向上、スタイルバイアスの影響など、複数の観点からその投資理論上の含意を検討することで、現代のポートフォリオ構築における実践的な意義を明らかにしたい。

3．等ウェイト投資戦略の有効性

本節では、等ウェイト投資戦略の有効性を示した代表的な学術論文4編を取り上げ、その理論的背景と実証的成果について概観する。

まず、DeMiguel et al.（2009）は、14銘柄の株式を対象に複数のポートフォリオ戦略を比較した包括的な研究を行っている。同研究では、平均分散最適化やベイズ推定など高度な手法と並べて、単純な等ウェイト戦略が最も安定的かつ高いパフォーマンスを示すことが明らかにされた。特筆すべきは、取引手数料を考慮した場合でも等ウェイト戦略の優位性が維持される点であり、実務的な示唆として、期待収益率の推定誤差やモデルの不安定性がパフォーマンスを損なう可能性を踏まえ、過度な最適化よりも分散性を重視した戦略の有用性が強調されている。

次に、Malladi and Fabozzi（2017）は、1927年から2014年までの長期実データとシミュレーションを用いて、時価総額加重平均型と等ウェイト型の投資戦略を比較した。同研究では、ブートストラップ法や実際のポートフォリオ構築を含む複数のシナリオにおいて、等ウェイト戦略が超過リターンやシャープ比率の面で一貫して高いパフォーマンスを示すことが確認された。特に、超過リターンを「サイズ効果」と「リバランス効果」に分解し、後者が主要な要因であることを明らかにした点は新規性が高く、等ウェイト戦略の構造的優位性を理論的に裏付ける成果といえる。

太田（2015）は、ファーマ・フレンチの6ファクターモデルを用いて、等ウェイト戦略の有効性をファクター投資の観点から分析している。まず、価格データからファクターの統計的性質を導出し、各ファクターに基づく投資スタイルの構造を精緻に把握した上で、ファクター間の相関が低い場合には等ウェイトによるリスク分散効果が顕著に働くことを示した。この結果は、ファクター投資におけるポートフォリオ構築の際に、等ウェイト戦略が有効な選択肢となり得ることを示唆している。

最後に、辻（2021）は、無作為に抽出された5銘柄から構成される3種類のポートフォリオ――ⅰ効率的ポートフォリオ、ⅱ最小分散ポートフォリオ、ⅲ等ウェイトポートフォリオ――について、実価格データを用いた大規模シミュレーション（70万回超）を実施し、事後的なパフォーマンスを評価した。その結果、等ウェイトポートフォリオが他の2戦略に対して圧倒的に高いパフォーマンスを示すことが確認され、単純な戦略であっても実務的に非常に有効である可能性が示された。

以上のように、等ウェイト投資戦略は、理論的にも実証的にも一定の有効性が認められており、特に推定誤差やモデル依存性が問題となる環境下では、実務的に魅力的な選択肢となり得る。

4．最適リバランス間隔

最後のトピックとして、ポートフォリオの再構築（リバランス）の在り方について考察する。等ウェイト戦略は、構成が単純で実装も容易である一方、資産価格の変動によりポートフォリオの比率が目標から乖離しやすいため、定期的なリバランスが不可欠である点に留意する必要がある。これは、時価総額加重平均型や株価平均型が、構築後に追加的な売買を伴わずとも自然にウェイトが調整されるのとは対照的である。なお、読売333の算出方法においては、「年3回、2月・5月・8月の最終金曜日の翌営業日に、ウェート調整日の前営業日の引け後に実施する」と定められており、四半期に近い頻度でリバランスが行われている。

リバランスの実施方法としては、等ウェイト戦略に限らず、一般的な投資戦略においても、主に以下の二つの手法が存在する。一つは、一定の時間間隔で実施する暦時間ベースの戦略であり、もう一つは、資産配分が目標から一定程度乖離した時点で実施する閾値ベースの戦略である。近年の研究では、後者の閾値ベース戦略の方が、取引コストを抑えつつリスク管理を強化できる点で優れているとする結果が多く報告されている。

一方、暦時間ベースのリバランス戦略においても、ポートフォリオのボラティリティ水準に応じてリバランス間隔を調整することが望ましいとする実証結果が多数存在する。例えば、Karabatı（2024）では、最適なリバランス間隔を理論的に導出しており、リバランスのタイミングはポートフォリオのボラティリティだけでなく投資期間（満期）、取引手数料などに応じて設定されるべきであると論じている。同論文によれば、平均的な最適リバランス頻度は年3〜5回程度とされており、読売333における年3回のリバランスは、理論的に導出された最適間隔から大きく逸脱しているわけではなく、実務的にも妥当な設計であると評価できる。

5．最後に

第3節で紹介した先行研究は、CAPMにおいて理論的に最適とされる時価総額加重平均ポートフォリオが、実証的には等ウェイトポートフォリオに劣後するという一見逆説的な現象に対して、一定の解答を与えている。特に注目すべきは、CAPMの根幹をなす仮定が現実の市場環境ではしばしば成立しない点であり、これが理論と実証の乖離を生む主要因と考えられる。

第一の、そして最も重要な解答は、モデルパラメータ――とりわけ期待収益率――の不確実性である。CAPMでは、全ての投資家が株式の収益に対して共通の同時分布を有しているという極めて強い仮定を置いており、これに基づいて市場均衡が導かれる。しかしながら、現実の市場では、期待収益率の推定には大きな誤差が伴い、推定値は時系列的にも不安定であることが広く知られている。こうした不確実性は、個々の投資家の最適化問題に影響を与えるのみならず、資産価格の形成や市場全体の均衡にも無視し得ない影響を及ぼすことが、近年の研究によって明らかにされつつある。

例えば、Hara and Honda（2022）は、モデルにおける期待収益率の不確実性を「確率分布の曖昧さ（ambiguity）」として定式化し、曖昧さを回避する投資家の行動を仮定した場合、小型株の期待収益率が曖昧さのない場合と比較して上昇することを、米国株式市場のデータを用いて実証的に示している。この結果は、構成銘柄に小型株の比率が相対的に高い等ウェイトポートフォリオが、時価総額加重型ポートフォリオよりも高いパフォーマンスを示す傾向にあることを説明する理論的根拠となり得る。

第二の解答は、収益率分布の非斉時性（non-stationarity）である。株式の収益率分布が市場環境や景気循環、政策変更などの外的要因によって時間的に変化するという理解は、実務的にも理論的にも自然なものである。収益率分布が非斉時的である場合、時価総額加重平均型のポートフォリオは、構成比率が市場の変化に対して受動的であるため、最適な投資戦略との乖離が生じやすくなる。一方、等ウェイト戦略は定期的なリバランスを通じて構成比率を均等に保つため、結果として市場環境の変化に対して柔軟に対応し、安定したパフォーマンスを示す可能性が高い。

さらに、非斉時性は収益率分布にファットテール（fat tails）をもたらすことが知られており、これは極端な価格変動が生じる確率が高まることを意味する。特に、時価総額加重型ポートフォリオでは、大型株の急落がポートフォリオ全体に与える影響が大きいため、ボラティリティが高くなる傾向がある。これに対して、等ウェイト戦略は構成銘柄の分散性が高く、極端な値動きの影響を相対的に緩和する効果が期待される。

前節で触れたスマート・ベータ戦略のように、等ウェイト構成に加えて投資家のリスク選好やスタイル特性に応じた調整を加えることで、より多様な投資戦略が設計可能となり、資産形成の選択肢が拡大することが期待されている。その意味でも、最も基本的かつ単純な戦略である等ウェイト投資戦略の構造的特徴や理論的性質について、今後さらに精緻な分析が進むことが望まれる。等ウェイト戦略は、単なるベンチマークの一形態にとどまらず、現代の不確実性の高い市場環境において、実務的にも理論的にも重要な投資手法であるといえよう。